Si të vërtetohet dhe vërtetohet se trekëndëshat janë kongruentë. Vërtetimet e teoremave për këndet që lidhen me rrethin Si të vërtetohet se këndet janë të barabartë

Udhëzimet

Nëse trekëndëshat ABC dhe DEF kanë brinjën AB të barabartë me brinjën DE, dhe këndet ngjitur me brinjën AB janë të barabartë me këndet ngjitur me brinjën DE, atëherë këta trekëndësha konsiderohen kongruentë.

Nëse trekëndëshat ABC kanë brinjë AB, BC dhe CD të barabarta me brinjët e tyre përkatëse të trekëndëshit DEF, atëherë këta trekëndësha janë kongruentë.

shënim

Nëse keni nevojë të provoni barazinë e dy trekëndëshave kënddrejtë, kjo mund të bëhet duke përdorur shenjat e mëposhtme të barazisë së trekëndëshave kënddrejtë:

Njëra nga këmbët dhe hipotenuza;
- në dy anët e njohura;
- përgjatë njërës prej këmbëve dhe këndit akut ngjitur me të;
- përgjatë hipotenuzës dhe njërit prej këndeve akute.

Trekëndëshat janë akute (nëse të gjitha këndet e tij janë më pak se 90 gradë), të mpirë (nëse njëri prej këndeve të tij është më shumë se 90 gradë), barabrinjës dhe dykëndësh (nëse dy nga brinjët e tij janë të barabarta).

Këshilla të dobishme

Përveç që trekëndëshat janë të barabartë me njëri-tjetrin, të njëjtët trekëndësha janë të ngjashëm. Trekëndësha të ngjashëm janë ata, këndet e të cilëve janë të barabartë me njëri-tjetrin, dhe brinjët e njërit trekëndësh janë në përpjesëtim me brinjët e tjetrit. Vlen të përmendet se nëse dy trekëndësha janë të ngjashëm me njëri-tjetrin, kjo nuk garanton barazinë e tyre. Kur pjesëtohen brinjët e ngjashme të trekëndëshave me njëra-tjetrën, llogaritet i ashtuquajturi koeficienti i ngjashmërisë. Ky koeficient mund të merret edhe duke pjesëtuar sipërfaqet e trekëndëshave të ngjashëm.

Burimet:

• vërtetojnë barazinë e sipërfaqeve të trekëndëshave

Dy trekëndësha janë të barabartë nëse të gjithë elementët e njërit janë të barabartë me elementët e tjetrit. Por nuk është e nevojshme të njihen të gjitha madhësitë e trekëndëshave për të nxjerrë një përfundim për barazinë e tyre. Mjafton të kemi grupe të caktuara parametrash për figurat e dhëna.

Udhëzimet

Nëse dihet se dy brinjë të njërit trekëndësh janë të barabartë me tjetrin dhe këndet ndërmjet këtyre brinjëve janë të barabartë, atëherë trekëndëshat në fjalë janë kongruentë. Për ta vërtetuar atë, rreshtoni kulmet e këndeve të barabarta të dy figurave. Vazhdoni shtresimin. Nga pika që rezulton e përbashkët për dy trekëndëshat, drejtoni njërën anë të këndit të trekëndëshit të mbivendosur përgjatë anës përkatëse të figurës së poshtme. Sipas kushteve, këto dy anë janë të barabarta. Kjo do të thotë që skajet e segmenteve do të përkojnë. Rrjedhimisht, një çift tjetër kulmesh në trekëndëshat e dhënë ka përkuar. Drejtimet e anëve të dyta të këndit nga i cili filloi do të përkojnë për shkak të barazisë së këtyre këndeve. Dhe meqenëse këto anë janë të barabarta, kulmi i fundit do të mbivendoset. Një vijë e vetme e drejtë mund të vizatohet midis dy pikave. Prandaj, anët e treta të dy trekëndëshave do të përkojnë. Ju keni marrë dy shifra plotësisht që përputhen dhe shenjën e parë të provuar të barazisë së trekëndëshave.

Nëse një brinjë dhe dy kënde ngjitur në një trekëndësh janë të barabartë me këndet përkatëse në një trekëndësh tjetër, atëherë këta dy trekëndësha janë kongruentë. Për të vërtetuar saktësinë e këtij pohimi, vendosni dy figura, duke rreshtuar kulmet e këndeve të barabarta me brinjë të barabarta. Për shkak të barazisë së këndeve, drejtimet e anëve të dytë dhe të tretë do të përkojnë dhe vendi i kryqëzimit të tyre do të përcaktohet pa mëdyshje, domethënë, kulmi i tretë i trekëndëshit të parë do të përkojë domosdoshmërisht me një pikë të ngjashme të e dyta. Është vërtetuar kriteri i dytë për barazinë e trekëndëshave.

Këtë herë propozoj të organizohet diçka si një “maratonë e bazuar në prova” për zgjidhjen e problemeve që u ofrohen nxënësve të klasës së nëntë në Provimin Akademik Shtetëror në matematikë. Ato lidhen me vërtetimin e fakteve gjeometrike të thjeshta, por në të njëjtën kohë shumë të dobishme. Artikulli qëllimisht nuk ofron zgjidhje të detajuara për problemet, vetëm disa skica dhe këshilla. Mundohuni ta kapërceni vetë këtë distancë maratonë, pa gabime dhe me një qasje.

Detyra 1. Vërtetoni se përgjysmorët e këndeve fqinjë janë pingul.

Këndi α caktohet nga një hark, β me dy

Dëshmi: nga figura duket qartë se α + α + β + β = 2α + 2β = 180 0 (kënd i drejtë), pra, α + β = 90 0 . Q.E.D.

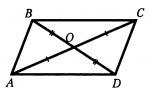
Detyra 2. Dy segmente A.C. Dhe BD kryqëzohen në një pikë O, e cila është mesi i secilit prej tyre. Vërtetoni barazinë e trekëndëshave ACD Dhe CAB.

ABCD, natyrisht, do të jetë një paralelogram, por kjo nuk është dhënë në kusht

Dëshmi: trekëndëshat anësorë janë të barabartë në dy brinjë dhe këndi ndërmjet tyre ( B.O. = O.D.- me kusht, A.O. = O.C.- sipas kushtit, ∠ DOC = ∠AOB- vertikale), që është ∠ ACD = ∠CAB, dhe meqenëse janë të shtrirë në mënyrë tërthore në vija të drejta AB, CD dhe sekant A.C., Kjo AB paralele DC. Në mënyrë të ngjashme vërtetojmë paralelizmin e drejtëzave B.C. Dhe A.D. Kështu që, ABCDështë një paralelogram sipas përkufizimit. B.C. = pas Krishtit, AB = CD(në një paralelogram, anët e kundërta janë të barabarta), A.C.- e zakonshme për trekëndëshat ACD Dhe CAB, pra janë të barabarta në tre anët. Q.E.D.

Detyra 3. Vërtetoni se mediana e tërhequr në bazën e një trekëndëshi dykëndësh është përgjysmues i këndit përballë bazës dhe është gjithashtu pingul me bazën.

Këndet e formuara nga mediana dhe baza do të quhen "të poshtme", mediana dhe anët - "sipërme"

Dëshmi: trekëndëshat anësor në figurë janë të barabartë në tre anët, nga ku rezulton se, së pari, këndet "e sipërme" janë të barabarta (ata vërtetuan se përgjysmuesja), së dyti, këndet "e poshtme", në total si ato ngjitur duke dhënë 180. 0, dhe për këtë arsye është e barabartë me 90 0 secila (perpendikulariteti i vërtetuar). Q.E.D.

Detyra 4. Vërtetoni se mesinat e tërhequra në brinjët anësore të një trekëndëshi dykëndësh janë të barabartë.

Trekëndëshat e formuar nga mediana, baza dhe gjysmat e poshtme të anëve anësore të trekëndëshit origjinal quhen "të poshtëm"

Dëshmi: këndet në bazën e një trekëndëshi dykëndësh janë të barabartë, prandaj trekëndëshat "të poshtëm" janë të barabartë në dy brinjë dhe këndi ndërmjet tyre, që nënkupton barazinë e ndërmjetësve të vizatuar. Q.E.D.

Detyra 5. Vërtetoni se përgjysmorët e nxjerrë nga kulmet e bazës së një trekëndëshi dykëndësh janë të barabartë.

Të gjitha këndet e shënuara në figurë janë, natyrisht, të barabarta, megjithëse ato tregohen nga harqe të ndryshme

Dëshmi: Trekëndëshi "poshtë" është dykëndësh, i cili rrjedh nga barazia e këndeve në bazën e tij, trekëndëshat "anësorë" janë të barabartë në brinjë (të barabartë nga përgjysmorët e provuar më sipër) dhe dy kënde (i pari është i barabartë nga kushti, i dyti. janë vertikale), prandaj edhe pjesët e mbetura të përgjysmuesve janë të barabarta me njëra-tjetrën, që do të thotë se të gjithë përgjysmuesit janë të barabartë. Q.E.D.

Detyra 6. Vërtetoni se gjatësia e segmentit që lidh mesin e dy brinjëve të një trekëndëshi është e barabartë me gjysmën e brinjës së tretë.

Anët e pastra do t'i quajmë "baza", ato të kryqëzuara - "anët"

Dëshmi: anët anësore të trekëndëshit të vogël dhe të madh në figurë lidhen si 1: 2, përveç kësaj, ato kanë një kënd të përbashkët, që do të thotë se ato janë të ngjashme në atributin e dytë me një koeficient ngjashmërie 1: 2, prandaj bazat janë të lidhura si 1: 2. Që është ajo që duhej vërtetuar.

Detyra 7. Vërtetoni se diagonalja e një paralelogrami e ndan atë në dy trekëndësha të barabartë.

Një paralelogram me një diagonale, ndoshta nuk ka asgjë më shumë për të shtuar

Dëshmi: Brinjët e kundërta të një paralelogrami janë të barabarta, diagonalja është brinja e përbashkët për këta trekëndësha, pra janë të barabarta në tre brinjë. Q.E.D.

Detyra 8. Vërtetoni se mediana e një trekëndëshi kënddrejtë të tërhequr nga hipotenuza është e barabartë me gjysmën e hipotenuzës.

Me fjalë të tjera, mediana është tërhequr nga kulmi i këndit të drejtë

Dëshmi: nëse përshkruajmë një rreth rreth një trekëndëshi të caktuar kënddrejtë, atëherë këndi i drejtë i trekëndëshit të brendashkruar në këtë rreth do të përshkruhet me një gjysmërreth, kështu që hipotenuza do të jetë diametri i këtij rrethi, dhe gjysmat e hipotenuzës dhe mediana e dhënë. tek ne në problem do të jenë rrezet, pra janë të gjithë të barabartë. Q.E.D.

Detyra 9. Vërtetoni se segmentet tangjente të tërhequra në një rreth nga një pikë janë të barabarta.

Ndërtimi shtesë: lidhni pikën C me pikën O (mendërisht)

Dëshmi: kënde B Dhe A vijat e drejta (rrezet e rrethit të tërhequr në pikën e lëkundjes janë pingul me tangjentet), që do të thotë trekëndësha kënddrejtë AOC Dhe BOC e barabartë në hipotenuzë (ana që imagjinojmë është e zakonshme për ta O.C.) dhe këmbën (rrezet e rrethit O.B. = O.A.), që do të thotë A.C. = C.B.. Q.E.D.

Problemi 10. Vërtetoni se diametri që kalon nga mesi i një korde të një rrethi është pingul me të.

Vija që lidh dy pika në figurë është mediana e trekëndëshit që do të shqyrtojmë

Dëshmi: në një trekëndësh dykëndësh të formuar nga pikat e kryqëzimit të një korde me një rreth dhe qendra e këtij rrethi, mesatarja e paraqitur do të jetë lartësia, që do të thotë se diametri që përmban këtë lartësi është pingul me kordën. Q.E.D.

Problemi 11. Vërtetoni se nëse dy rrathë kanë një kordë të përbashkët, atëherë vija që kalon nga qendra e këtyre rrathëve është pingul me këtë kordë.

Lidhni mendërisht së bashku të gjitha pikat e shënuara në figurë, le të quajmë pikën e kryqëzimit të H horizontale dhe vertikale

Dëshmi: trekëndëshat O 1 A.O. 2 dhe O 1 B.O. 2 janë të barabarta në tre anët, pra, ∠ HO 2 A = ∠HO 2 B, pastaj trekëndëshat HAO 2 dhe HBO 2 janë të barabarta në të dyja anët dhe këndi ndërmjet tyre, që do të thotë ∠ AHO 2 = ∠BHO 2, dhe në total dy kënde të barabarta mund të japin 180 0 vetëm nëse secili prej tyre është i barabartë me 90 0. Q.E.D.

Problemi 12. Vërtetoni se nëse një rreth mund të futet në një katërkëndësh, atëherë shumat e gjatësive të brinjëve të kundërta të tij janë të barabarta.

Katërkëndësh i rrethuar. Le ta quajmë ABCD. Le të jenë M, E, X dhe L pika tangjente

Dëshmi: Ne përdorim teoremën për segmentet tangjente (Problemi 9). QV = VR, SR = CH, DX = D.L. Dhe AT = AK. Le të përmbledhim anët AB Dhe CD: AB + CD= (JAM.+ M.B.) + (DX+ XC) = AL+ BE+ D.L.+ C.E.= (AL+ LD) + (BE+ E.C.) = pas Krishtit+ B.C. Q.E.D.

Problemi 13. Vërtetoni se nëse një rreth mund të rrethohet rreth një katërkëndëshi, atëherë shumat e këndeve të tij të kundërta janë të barabarta.

rrethi

Dëshmi: Sipas teoremës së këndit të brendashkruar, shuma e këndeve të kundërta të këtij katërkëndëshi është e barabartë me 180 0, pasi së bashku ato qëndrojnë në një rreth të plotë, masa e shkallës së të cilit është 360 0. Q.E.D.

Problemi 14. Vërtetoni se nëse një rreth mund të rrethohet rreth një trapezi, atëherë trapezi është dykëndor.

Dëshmi: shuma e këndeve të kundërta të një katërkëndëshi të brendashkruar në rreth është e barabartë me α + β = 180 0 (shih problemin 13), shuma e këndeve në anën anësore të trapezit është gjithashtu e barabartë me α + γ = 180 0 (këto kënde janë të njëanshëm me baza paralele dhe një brinjë sekante), nga krahasimi i këtyre formulave gjejmë se β = γ d.m.th., këndet në bazën e një trapezi të tillë janë të barabarta, dhe ai është me të vërtetë dykëndor. Q.E.D.

Problemi 15. Në katror ABCD pikë TE Dhe E- pikat e mesit të anëve AB Dhe pas Krishtit përkatësisht. Vërtetoni këtë KD pingul C.E..

Teorema 1 . Madhësia e këndit të brendashkruar është e barabartë me gjysmën e madhësisë së këndit qendror të nënshtruar nga i njëjti hark.

Dëshmi . Le të shqyrtojmë së pari këndin e mbishkruar ABC, anash B.C. që është diametri i rrethit dhe këndi qendror AOC(Fig. 5).

Që nga segmentet A.O. Dhe B.O. janë rrezet e rrethit, pastaj trekëndëshi AOB– izosceles, dhe këndi ABO e barabartë me këndin OAB. Sepse këndi AOCështë këndi i jashtëm i trekëndëshit AOB, atëherë barazitë janë të vërteta

Kështu, në rastin kur njëra nga brinjët e këndit të brendashkruar kalon nga qendra e rrethit, vërtetohet teorema 1.

Tani merrni parasysh rastin kur qendra e rrethit shtrihet brenda këndit të brendashkruar (Fig. 6).

dhe Teorema 1 vërtetohet në këtë rast.

Mbetet të shqyrtohet rasti kur qendra e rrethit shtrihet jashtë këndit të brendashkruar (Fig. 7).

Në këtë rast barazitë janë të vërteta

e cila plotëson vërtetimin e Teoremës 1.

Teorema 2 . Madhësia e këndit të formuar nga kordat e kryqëzuara është e barabartë me gjysmën e shumës së madhësive të harqeve të mbyllura midis anëve të tij.

Dëshmi . Merrni parasysh figurën 8.

Ne jemi të interesuar për këndin AED E akorde AB Dhe CD. Sepse këndi AED– këndi i jashtëm i një trekëndëshi SHTRAT, dhe këndet CDB Dhe ABD

Q.E.D.

Teorema 3 . Madhësia e këndit të formuar nga sekantet që kryqëzohen jashtë rrethit është e barabartë me gjysmën e ndryshimit në madhësitë e harqeve të mbyllura midis anëve të këtij këndi.

Dëshmi . Merrni parasysh figurën 9.

Ne jemi të interesuar për këndin SHTRAT, i formuar duke u prerë në një pikë E sekante AB Dhe CD. Sepse këndi ADC– këndi i jashtëm i një trekëndëshi ADE, dhe këndet ADC , DCB Dhe DAB janë kënde të brendashkruara, atëherë barazitë janë të vërteta

Q.E.D.

Teorema 4 . Madhësia e këndit të formuar nga një tangjente dhe një kordë që kalon nëpër pikën e kontaktit është e barabartë me gjysmën e madhësisë së harkut të mbyllur midis anëve të tij.

Dëshmi . Merrni parasysh figurën 10.

Ne jemi të interesuar për këndin BAC e formuar nga tangjentja AB dhe akord A.C.. Sepse pas Krishtitështë diametri që kalon nëpër pikën e kontaktit dhe këndi ACDështë një kënd i brendashkruar në bazë të diametrit, pastaj këndeve DAB Dhe DCA– drejt. Prandaj barazitë janë të vërteta

Q.E.D.

Teorema 5 . Madhësia e këndit të formuar nga një tangjente dhe një sekant është e barabartë me gjysmën e ndryshimit në madhësitë e harqeve të mbyllura midis anëve të këtij këndi.

Dëshmi . Merrni parasysh figurën 11.

Ne jemi të interesuar për këndin SHTRAT e formuar nga tangjentja AB dhe sekant CD. Vini re se këndi BDC– këndi i jashtëm i një trekëndëshi DBE, dhe këndet BDC Dhe BCD janë kënde të brendashkruara. Për më tepër, këndet DBE Dhe DCB, në bazë të Teoremës 4, janë të barabarta. Prandaj barazitë janë të vërteta

Dy kënde quhen ngjitur nëse kanë një anë të përbashkët, dhe anët e tjera të këtyre këndeve janë rreze plotësuese. Në figurën 20, këndet AOB dhe BOC janë ngjitur.

Shuma e këndeve ngjitur është 180°

Teorema 1. Shuma e këndeve ngjitur është 180°.

Dëshmi. Trau OB (shih Fig. 1) kalon midis anëve të këndit të shpalosur. Kjo është arsyeja pse ∠ AOB + ∠ BOS = 180°.

Nga teorema 1 rezulton se nëse dy kënde janë të barabartë, atëherë këndet e tyre ngjitur janë të barabartë.

Këndet vertikale janë të barabarta

Dy kënde quhen vertikale nëse brinjët e njërit kënd janë rreze plotësuese të brinjëve të tjetrit. Këndet AOB dhe COD, BOD dhe AOC, të formuara në kryqëzimin e dy vijave të drejta, janë vertikale (Fig. 2).

Teorema 2. Këndet vertikale janë të barabarta.

Dëshmi. Le të shqyrtojmë këndet vertikale AOB dhe COD (shih Fig. 2). Këndi BOD është ngjitur me secilin nga këndet AOB dhe COD. Nga teorema 1 ∠ AOB + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.

Nga kjo arrijmë në përfundimin se ∠ AOB = ∠ COD.

Përfundim 1. Një kënd ngjitur me një kënd të drejtë është një kënd i drejtë.

Le të shqyrtojmë dy drejtëza të kryqëzuara AC dhe BD (Fig. 3). Ata formojnë katër qoshe. Nëse njëri prej tyre është i drejtë (këndi 1 në figurën 3), atëherë këndet e mbetura janë gjithashtu të drejta (këndet 1 dhe 2, 1 dhe 4 janë ngjitur, këndet 1 dhe 3 janë vertikalë). Në këtë rast, ata thonë se këto drejtëza kryqëzohen në kënde të drejta dhe quhen pingule (ose reciprokisht pingul). Perpendikulariteti i drejtëzave AC dhe BD shënohet si më poshtë: AC ⊥ BD.

Një përgjysmues pingul me një segment është një drejtëz pingul me këtë segment dhe që kalon nga mesi i tij.

AN - pingul me një vijë

Konsideroni një drejtëz a dhe një pikë A të mos shtrirë mbi të (Fig. 4). Le të lidhim pikën A me një segment me pikën H me drejtëz a. Segmenti AN quhet pingul i tërhequr nga pika A në drejtëzën a nëse drejtëzat AN dhe a janë pingule. Pika H quhet baza e pingules.

Vizatim katror

Teorema e mëposhtme është e vërtetë.

Teorema 3. Nga çdo pikë që nuk shtrihet në një vijë, është e mundur të vizatoni një pingul me këtë drejtëz dhe, për më tepër, vetëm një.

Për të vizatuar një pingul nga një pikë në një vijë të drejtë në një vizatim, përdorni një katror vizatimi (Fig. 5).

Komentoni. Formulimi i teoremës zakonisht përbëhet nga dy pjesë. Një pjesë flet për atë që jepet. Kjo pjesë quhet kushti i teoremës. Pjesa tjetër flet për atë që duhet të vërtetohet. Kjo pjesë quhet përfundimi i teoremës. Për shembull, kushti i Teoremës 2 është që këndet të jenë vertikale; përfundim - këto kënde janë të barabarta.

Çdo teoremë mund të shprehet në detaje me fjalë, në mënyrë që gjendja e saj të fillojë me fjalën "nëse" dhe përfundimi i saj me fjalën "atëherë". Për shembull, Teorema 2 mund të shprehet në detaje si më poshtë: "Nëse dy kënde janë vertikale, atëherë ato janë të barabarta".

Shembulli 1. Një nga këndet ngjitur është 44°. Me çfarë barazohet tjetri?

Zgjidhje. Le të shënojmë masën e shkallës së një këndi tjetër me x, atëherë sipas teoremës 1.
44° + x = 180°.
Duke zgjidhur ekuacionin që rezulton, gjejmë se x = 136°. Prandaj, këndi tjetër është 136°.

Shembulli 2. Le të jetë këndi COD në figurën 21 45°. Cilat janë këndet AOB dhe AOC?

Zgjidhje. Këndet COD dhe AOB janë vertikale, prandaj sipas teoremës 1.2 janë të barabartë, d.m.th. ∠ AOB = 45°. Këndi AOC është ngjitur me këndin COD, që do të thotë sipas Teoremës 1.
∠ AOC = 180° - ∠ COD = 180° - 45° = 135°.

Shembulli 3. Gjeni kënde ngjitur nëse njëri prej tyre është 3 herë më i madh se tjetri.

Zgjidhje. Le të shënojmë masën e shkallës së këndit më të vogël me x. Atëherë masa e shkallës së këndit më të madh do të jetë 3x. Meqenëse shuma e këndeve ngjitur është e barabartë me 180° (teorema 1), atëherë x + 3x = 180°, prej nga x = 45°.
Kjo do të thotë se këndet ngjitur janë 45° dhe 135°.

Shembulli 4. Shuma e dy këndeve vertikale është 100°. Gjeni madhësinë e secilit prej katër këndeve.

Zgjidhje. Le të korrespondojnë kushtet e problemit me figurën 2. Këndet vertikale COD me AOB janë të barabarta (teorema 2), që do të thotë se edhe masat e shkallës së tyre janë të barabarta. Prandaj, ∠ COD = ∠ AOB = 50° (shuma e tyre sipas kushtit është 100°). Këndi BOD (gjithashtu këndi AOC) është ngjitur me këndin COD, dhe për këtë arsye, nga Teorema 1
∠ BOD = ∠ AOC = 180° - 50° = 130°.