Як встановити та довести, що трикутники рівні. Докази теорем про кути, пов'язані з колом

Інструкція

Якщо у трикутників ABC і DEF сторона AB дорівнює стороні DE, а кути, прилеглі до сторони AB, дорівнюють кутам, прилеглим до сторони DE, ці трикутники вважаються рівними.

Якщо у трикутників ABC сторони AB, BC і CD рівні відповідним сторонам трикутника DEF, то дані трикутники рівні.

Зверніть увагу

Якщо потрібно довести рівність між собою двох прямокутних трикутників, це можна зробити за допомогою наступних ознак рівності прямокутних трикутників:

По одному з катетів та гіпотенузі;
- за двома відомими катетами;
- по одному з катетів і гострому кутку, що прилягає до нього;
- з гіпотенузи та одного з гострих кутів.

Трикутники бувають гострокутними (якщо всі кути його менше 90 градусів), тупокутними (якщо один з його кутів більше 90 градусів), рівносторонніми та рівнобедреними (якщо дві сторони його рівні).

Корисна порада

Крім рівності трикутників між собою, ці трикутники є подібними. Подібними трикутниками вважаються ті, у яких кути рівні між собою, а сторони одного трикутника пропорційні сторонам іншого. Варто зазначити, що якщо два трикутники подібні між собою, то це не гарантує їхньої рівності. При розподілі подібних сторін трикутників одне одного розраховується так званий коефіцієнт подоби. Також цей коефіцієнт можна отримати шляхом розподілу площ таких трикутників.

Джерела:

• довести рівність площ трикутників

Два трикутники рівні, якщо всі елементи одного дорівнюють елементам іншого. Але необов'язково знати всі розміри трикутників, щоб зробити висновок про їхню рівність. Достатньо мати певні набори параметрів заданих фігур.

Інструкція

Якщо відомо, що дві сторони одного трикутника рівні іншого і рівні кути між цими сторонами, трикутники, що розглядаються, рівні. Для доказу поєднайте вершини рівних кутів двох фігур. Продовжуйте накладення. З отриманої загальної для двох трикутників точки направте одну сторону кута накладеного трикутника по відповідній стороні нижньої фігури. За умовою, ці сторони у двох рівні. Значить кінці відрізків збігатимуться. Отже, поєдналася ще одна пара вершин у заданих трикутниках. Напрямки других сторін кута, з якого розпочато, збігатимуться внаслідок рівності цих кутів. Оскільки ці сторони рівні, відбудеться накладення останньої вершини. Між двома точками можливе проведення єдиної прямої. Отже, треті сторони у двох трикутниках збігатимуться. Ви отримали дві фігури, що повністю збіглися, і доведена перша ознака рівності трикутників.

Якщо сторона та прилеглі до неї два кути в одному трикутнику рівні відповідним в іншому трикутнику, то ці два трикутники рівні. Для доказу правильності цього твердження накладіть дві фігури, поєднавши вершини рівних кутів при рівних сторонах. Внаслідок рівності кутів збігається напрямок другої та третьої сторін і однозначно визначиться місце їх перетину, тобто третя вершина першого з трикутників обов'язково поєднається з аналогічною точкою другого. Друга ознака рівності трикутників доведена.

Пропоную цього разу влаштувати щось на кшталт «доказового марафону» щодо вирішення завдань, які пропонуються дев'ятикласникам у варіантах ДПА з математики. Пов'язані вони з підтвердженням нескладних, але водночас дуже корисних геометричних фактів. У статті навмисно не наведено докладних розв'язків задач, лише деякі нариси та підказки. Намагайтеся подолати цю марафонську дистанцію самостійно, без помилок і за один підхід.

Завдання 1.Доведіть, що бісектриси суміжних кутів перпендикулярні.

Кут α позначений однією дугою, β - двома

Доведення:з малюнка видно, що α + α + β + β = 2α + 2β = 180 0 (розгорнутий кут), отже, α + β = 90 0 . Що й потрібно було довести.

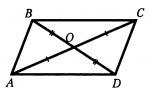
Завдання 2.Два відрізки ACі BDперетинаються у точці Oяка є серединою кожного з них. Доведіть рівність трикутників ACDі CAB.

ABCD, звичайно, буде паралелограмом, але за умови цього не дано

Доведення:бічні трикутники рівні по двох сторонах і кут між ними ( BO = OD- за умовою, AO = OC- За умовою, ∠ DOC = ∠AOBвертикальні), тобто ∠ ACD = ∠CAB, а оскільки вони є навхрест лежачими при прямих AB, CDі січеною AC, то ABпаралельна DC. Аналогічно доводимо паралельність прямих BCі AD.Отже, ABCD- Паралелограм за визначенням. BC = AD, AB = CD(У паралелограмі протилежні сторони рівні), AC- загальна для трикутників ACDі CABтому вони рівні по трьох сторонах. Що й потрібно було довести.

Завдання 3.Доведіть, що медіана, проведена до основи рівнобедреного трикутника, є бісектрисою кута, що протилежить основі, а також перпендикулярна основі.

Кути, утворені медіаною та основою, назвемо «нижніми», медіаною та бічними сторонами — «верхніми»

Доведення:бічні трикутники на малюнку рівні по трьох сторонах, з чого випливає рівність, по-перше, «верхніх» кутів (довели, що бісектриса), по-друге, «нижніх» кутів, у сумі як суміжні 180 0 , і рівних тому по 90 0 кожен (довели перпендикулярність). Що й потрібно було довести.

Завдання 4.Доведіть, що медіани, проведені до бокових сторін рівнобедреного трикутника, дорівнюють.

Трикутники, утворені медіанами, основою та нижніми половинами бічних сторін вихідного трикутника, назвемо «нижніми»

Доведення:кути при підставі рівнобедреного трикутника рівні, тому «нижні» трикутники рівні по двох сторонах і кут між ними, з чого випливає рівність проведених медіан. Що й потрібно було довести.

Завдання 5.Доведіть, що бісектриси, проведені з вершин основи рівнобедреного трикутника, рівні.

Усі відзначені малюнку кути, звісно, ​​рівні, хоч і позначені різними дугами

Доведення:«нижній» трикутник рівнобедрений, що випливає з рівності кутів при його підставі, «бічні» трикутники рівні по стороні (рівні з доведеного вище частинки бісектрис) і двом кутам (перші рівні за умовою, другі як вертикальні), тому частинки, що залишилися, бісектрис також рівні одне одному, отже рівні й самі бісектриси цілком. Що й потрібно було довести.

Завдання 6.Доведіть, що довжина відрізка, що з'єднує середини двох сторін трикутника, дорівнює половині третьої сторони.

Чистенькі сторони назвемо «підставами», перекреслені - «бічними сторонами»

Доведення:бічні сторони маленького і великого трикутника на малюнку відносяться як 1: 2, крім того, у них є один загальний кут, а значить вони подібні за другою ознакою з коефіцієнтом подібності 1: 2, тому й підстави відносяться як 1: 2. Що й вимагалося довести .

Завдання 7.Доведіть, що діагональ паралелограма розбиває його на два рівні трикутники.

Паралелограм з діагоналлю, більше, мабуть, нічого додати

Доведення:Протилежні сторони паралелограма рівні, діагональ є загальною стороною для цих трикутників, тому вони рівні по трьох сторонах. Що й потрібно було довести.

Завдання 8.Доведіть, що медіана, прямокутного трикутника, проведена до гіпотенузи, дорівнює половині гіпотенузи.

Тобто медіана проведена з вершини прямого кута

Доведення:якщо навколо даного прямокутного трикутника описати коло, то вписаний в це коло прямий кут трикутника буде описатися на півколо, тому гіпотенуза буде діаметром цього кола, а половинки гіпотенузи і дана нам в задачі медіана - радіусами, отже, всі вони рівні. Що й потрібно було довести.

Завдання 9.Доведіть, що відрізки дотичних, проведених до кола з однієї точки, рівні.

Додаткова побудова: з'єднуємо точку C з точкою O (подумки)

Доведення:кути Bі Aпрямі (радіуси кола, проведені в точку гойдання, перпендикулярні дотичним), означає прямокутні трикутники AOCі BOCрівні з гіпотенузи (загальна для них уявна сторона OC) та катету (радіуси кола OB = OA), а значить AC = CB. Що й потрібно було довести.

Завдання 10.Доведіть, що діаметр, що проходить через середину хорди кола, перпендикулярний їй.

Лінія, що з'єднує дві точки на малюнку, є медіаною трикутника, яку ми розглянемо

Доведення:в рівнобедреному трикутнику, утвореному точками перетину хорди з колом і центром цього кола, зображена медіана буде висотою, а значить діаметр, що містить у собі цю висоту, перпендикулярний хорді. Що й потрібно було довести.

Завдання 11.Доведіть, що якщо два кола мають загальну хорду, то пряма, яка проходить через центр цих кіл, перпендикулярна даній хорді.

Подумки з'єднуємо разом всі зазначені малюнку точки, точку перетину горизонталі і вертикалі назвемо H

Доведення:трикутники O 1 AO 2 та O 1 BO 2 рівні по трьох сторонах, отже, ∠ HO 2 A = ∠HO 2 Bтоді трикутники HAO 2 та HBO 2 рівні по двох сторонах і кут між ними, значить ∠ AHO 2 = ∠BHO 2 , а в сумі два рівні кути можуть давати 180 0 тільки в тому випадку, якщо кожен з них дорівнює по 90 0 . Що й потрібно було довести.

Завдання 12.Доведіть, що якщо чотирикутник можна вписати коло, то суми довжин його протилежних сторін рівні.

Описаний чотирикутник. Назвемо його ABCD. Нехай M, E, X та L — точки дотику

Доведення:використовуємо теорему про відрізки дотичних (завдання 9). ВК = ВР, СР = СН, DX = DLі АТ = АК. Підсумовуємо сторони АВі CD: AB + CD= (AM+ MB) + (DX+ XC) = AL+ BE+ DL+ CE= (AL+ LD) + (BE+ EC) = AD+ BC.Що й потрібно було довести.

Завдання 13.Доведіть, якщо близько чотирикутника можна описати коло, то суми його протилежних кутів рівні.

Описане коло

Доведення:за теоремою про вписаний кут сума протилежних кутів цього чотирикутника дорівнює 180 0 , оскільки разом вони спираються на повне коло, градусна міра якого 360 0 . Що й потрібно було довести.

Завдання 14.Доведіть, що якщо біля трапеції можна описати коло, то трапеція є рівнобедреною.

Доведення:сума протилежних кутів чотирикутника, вписаного в коло, дорівнює α + β = 180 0 (див. задачу 13), сума кутів при бічній стороні трапеції також дорівнює α + γ = 180 0 (ці кути є односторонніми при паралельних основах і січній бічній стороні), з порівняння цих формул отримуємо, що β = γ тобто кути при підставі такої трапеції рівні, і вона дійсно рівнобедрена. Що й потрібно було довести.

Завдання 15.В квадраті ABCDкрапки Доі Е- середини сторін АВі ADвідповідно. Довести, що КDперпендикулярна CE.

Теорема 1 . Величина вписаного кута дорівнює половині величини центрального кута, що спирається на ту саму дугу.

Доведення . Розглянемо спочатку вписаний кут ABC, сторона BCякого є діаметром кола, і центральний кут AOC(Рис. 5).

Оскільки відрізки AOі BOє радіусами кола, то трикутник AOB- рівнобедрений, і кут ABOдорівнює куту OAB. Оскільки кут AOCє зовнішнім кутом трикутника AOB, то справедливі рівність

Таким чином, у разі коли одна зі сторін вписаного кута проходить через центр кола, теорема 1 доведена.

Тепер розглянемо випадок, коли центр кола лежить усередині вписаного кута (рис. 6).

та теорема 1 у цьому випадку доведена.

Залишилося розглянути випадок, коли центр кола лежить поза вписаним кутом (рис. 7).

І тут справедливі рівності

що й завершує підтвердження теореми 1.

Теорема 2 . Величина кута, утвореного хордами, що перетинаються, дорівнює половині суми величин дуг, укладених між його сторонами.

Доведення . Розглянемо рисунок 8.

Нас цікавить величина кута AED Eхордами ABі CD. Оскільки кут AED- Зовнішній кут трикутника BED, а кути CDBі ABD

що й потрібно було довести.

Теорема 3 . Величина кута, утвореного січними, що перетинаються поза колом, дорівнює половині різниці величин дуг, укладених між сторонами цього кута.

Доведення . Розглянемо рисунок 9.

Нас цікавить величина кута BED, утвореного перетинаються в точці Eсічними ABі CD. Оскільки кут ADC- Зовнішній кут трикутника ADE, а кути ADC , DCBі DABє вписаними кутами, то справедливі рівності

що й потрібно було довести.

Теорема 4 . Величина кута, утвореного дотичною і хордою, що проходить через точку дотику, дорівнює половині величини дуги, укладеної між його сторонами.

Доведення . Розглянемо рисунок 10.

Нас цікавить величина кута BAC, утвореного щодо ABі хордий AC. Оскільки AD-діаметр, що проходить через точку торкання, а кут ACD- Вписаний кут, що спирається на діаметр, то кути DABі DCA- Прямі. Тому справедливі рівності

що й потрібно було довести

Теорема 5 . Величина кута, утвореного дотичною та січною, дорівнює половині різниці величин дуг, укладених між сторонами цього кута.

Доведення . Розглянемо рисунок 11.

Нас цікавить величина кута BED, утвореного щодо ABі січеною CD. Зауважимо, що кут BDC- Зовнішній кут трикутника DBE, а кути BDCі BCDє вписаними кутами. Крім того, кути DBEі DCB, Через теореми 4, рівні. Тому справедливі рівності

Два кути називаються суміжними, якщо в них одна сторона загальна, інші сторони цих кутів є додатковими променями. На малюнку 20 кути АОВ та ВОС суміжні.

Сума суміжних кутів дорівнює 180 °

Теорема 1. Сума суміжних кутів дорівнює 180 °.

Доведення. Промінь ОВ (див. рис.1) проходить між сторонами розгорнутого кута. Тому ∠ АОВ + ∠ ВОС = 180 °.

З теореми 1 випливає, що якщо два кути дорівнюють, то суміжні з ними кути рівні.

Вертикальні кути рівні

Два кути називаються вертикальними, якщо сторони одного кута є додатковими променями сторін іншого. Кути АОВ та COD, BOD та АОС, утворені при перетині двох прямих, є вертикальними (рис. 2).

Теорема 2. Вертикальні кути рівні.

Доведення. Розглянемо вертикальні кути АОВ та COD (див. рис. 2). Кут BOD є суміжним для кожного з кутів АОВ та COD. По теоремі 1 ∠ АОВ + ∠ BOD = 180 °, ∠ COD + ∠ BOD = 180 °.

Звідси укладаємо, що АОВ = ∠ COD.

Наслідок 1. Кут, суміжний із прямим кутом, є прямий кут.

Розглянемо дві прямі АС і BD, що перетинаються (рис.3). Вони утворюють чотири кути. Якщо один із них прямий (кут 1 на рис.3), то інші кути також прямі (кути 1 і 2, 1 і 4 - суміжні, кути 1 і 3 - вертикальні). І тут кажуть, що це прямі перетинаються під прямим кутом і називаються перпендикулярними (чи взаємно перпендикулярними). Перпендикулярність прямих АС та BD позначається так: AC ⊥ BD.

Серединним перпендикуляром до відрізка називається пряма, перпендикулярна до цього відрізка і через його середину.

АН - перпендикуляр до прямої

Розглянемо пряму а і точку А, яка не лежить на ній (рис.4). З'єднаємо точку А відрізком із точкою Н прямою а. Відрізок АН називається перпендикуляром, проведеним з точки А до прямої, якщо прямі АН і а перпендикулярні. Точка Н називається основою перпендикуляра.

Креслярський косинець

Справедлива наступна теорема.

Теорема 3. З будь-якої точки, що не лежить на прямій, можна провести перпендикуляр до цієї прямої, і до того ж тільки один.

Для проведення на кресленні перпендикуляра з точки прямої використовують креслярський косинець (рис.5).

Зауваження. Формулювання теореми зазвичай складається із двох частин. В одній частині йдеться про те, що дано. Ця частина називається умовою теореми. В іншій частині йдеться про те, що має бути доведено. Ця частина називається укладанням теореми. Наприклад, умова теореми 2 - вертикальні кути; висновок – ці кути рівні.

Будь-яку теорему можна докладно висловити словами отже її умова буде починатися словом «якщо», а висновок - словом «то». Наприклад, теорему 2 можна докладно висловити так: «Якщо два кути вертикальні, то вони рівні».

приклад 1.Один із суміжних кутів дорівнює 44°. Чому дорівнює інший?

Рішення. Позначимо градусну міру іншого кута через x тоді відповідно до теореми 1.
44 ° + х = 180 °.
Вирішуючи отримане рівняння, знаходимо, що х = 136 °. Отже, інший кут дорівнює 136 °.

приклад 2.Нехай малюнку 21 кут COD дорівнює 45°. Чому рівні кути АОВ та АОС?

Рішення. Кути COD та АОВ вертикальні, отже, за теоремою 1.2 вони рівні, тобто ∠ АОВ = 45°. Кут АОС суміжний з кутом COD, отже, теорема 1.
∠ АОС = 180 ° - ∠ COD = 180 ° - 45 ° = 135 °.

приклад 3.Знайти суміжні кути, якщо один з них у 3 рази більший за інший.

Рішення. Позначимо градусну міру меншого кута через х. Тоді градусний захід більшого кута буде Зх. Оскільки сума суміжних кутів дорівнює 180° (теорема 1), то х + Зх = 180°, звідки х = 45°.
Значить, суміжні кути дорівнюють 45 ° і 135 °.

приклад 4.Сума двох вертикальних кутів дорівнює 100 °. Знайти величину кожного із чотирьох кутів.

Рішення. Нехай умові задачі відповідає рисунок 2. Вертикальні кути COD до АОВ рівні (теорема 2), отже, рівні їх градусні заходи. Тому ∠ COD = ∠ АОВ = 50 ° (їх сума за умовою 100 °). Кут BOD (також і кут АОС) суміжний з кутом COD, і, отже, теорема 1
∠ BOD = ∠ АОС = 180 ° - 50 ° = 130 °.