Kako ugotoviti in dokazati, da so trikotniki skladni. Dokazi izrekov o kotih, povezanih s krogom. Kako dokazati, da so koti enaki

Navodila

Če imata trikotnika ABC in DEF stranico AB enako stranici DE in so koti, ki mejijo na stranico AB, enaki kotom, ki mejijo na stranico DE, se ti trikotniki štejejo za skladne.

Če imajo trikotniki ABC stranice AB, BC in CD enake pripadajočim stranicam trikotnika DEF, so ti trikotniki skladni.

Opomba

Če morate dokazati enakost dveh pravokotnih trikotnikov, lahko to storite z uporabo naslednjih znakov enakosti pravokotnih trikotnikov:

Ena od nog in hipotenuze;
- na dveh znanih straneh;
- vzdolž enega od krakov in ostrega kota ob njem;
- vzdolž hipotenuze in enega od ostrih kotov.

Trikotniki so ostri (če so vsi njegovi koti manjši od 90 stopinj), topi (če je eden od njegovih kotov večji od 90 stopinj), enakostranični in enakokraki (če sta mu dve strani enaki).

Koristen nasvet

Poleg tega, da sta trikotnika med seboj enaka, sta si enaka trikotnika podobna. Podobni trikotniki so tisti, katerih koti so med seboj enaki, stranice enega trikotnika pa so sorazmerne s stranicami drugega. Omeniti velja, da če sta dva trikotnika podobna drug drugemu, to ne zagotavlja njune enakosti. Pri delitvi podobnih strani trikotnikov med seboj se izračuna tako imenovani koeficient podobnosti. Ta koeficient lahko dobimo tudi z delitvijo ploščin podobnih trikotnikov.

Viri:

• dokaži enakost ploščin trikotnikov

Dva trikotnika sta enaka, če so vsi elementi enega enaki elementom drugega. Vendar ni treba poznati vseh velikosti trikotnikov, da bi lahko sklepali o njihovi enakosti. Dovolj je imeti določene nize parametrov za dane številke.

Navodila

Če je znano, da sta dve stranici enega trikotnika enaki drugi in sta kota med tema stranicama enaka, potem sta zadevna trikotnika skladna. Da bi to dokazali, poravnajte oglišča enakih kotov dveh likov. Nadaljujte s plastenjem. Iz nastale točke, ki je skupna obema trikotnikoma, usmerite eno stran vogala prekrivajočega se trikotnika vzdolž ustrezne strani spodnje figure. Po pogoju sta ti dve strani enakovredni. To pomeni, da bodo konci segmentov sovpadali. Posledično je sovpadal še en par oglišč v danih trikotnikih. Smeri drugih strani kota, iz katerega se je začel, bodo sovpadale zaradi enakosti teh kotov. In ker sta ti stranici enaki, se bo zadnje oglišče prekrivalo. Med dvema točkama lahko narišemo eno ravno črto. Zato bosta tretji strani obeh trikotnikov sovpadali. Prejeli ste dva popolnoma ujemata lika in dokazano prvo znamenje enakosti trikotnikov.

Če so stranica in dva sosednja kota v enem trikotniku enaki ustreznim kotom v drugem trikotniku, sta ta dva trikotnika skladna. Da bi dokazali pravilnost te izjave, postavite dve sliki, tako da poravnate oglišča enakih kotov z enakimi stranicami. Zaradi enakosti kotov bosta smeri druge in tretje stranice sovpadali in kraj njunega presečišča bo nedvoumno določen, to pomeni, da bo tretje oglišče prvega od trikotnikov nujno sovpadalo s podobno točko trikotnika. drugo. Drugi kriterij za enakost trikotnikov je dokazan.

Tokrat predlagam, da bi organizirali nekaj takega kot »z dokazi podprt maraton« za reševanje nalog, ki jih ponujajo devetošolcem pri državnem izpitu iz matematike. Povezani so z dokazovanjem preprostih, a hkrati zelo uporabnih geometrijskih dejstev. Članek namenoma ne ponuja podrobnih rešitev problemov, le nekaj skic in nasvetov. Poskusite premagati to maratonsko razdaljo sami, brez napak in v enem pristopu.

Naloga 1. Dokaži, da so simetrale sosednjih kotov pravokotne.

Kot α je označen z enim lokom, β z dvema

Dokaz: iz slike je razvidno, da α + α + β + β = 2α + 2β = 180 0 (ravni kot), torej α + β = 90 0 . Q.E.D.

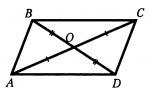
Naloga 2. Dva segmenta A.C. in BD sekajo v točki O, ki je sredina vsakega od njih. Dokaži enakost trikotnikov ACD in KABINA.

ABCD bo seveda paralelogram, vendar to ni podano v pogoju

Dokaz: stranski trikotniki so enaki v dveh stranicah in v kotu med njima ( B.O. = O.D.- po pogoju, A.O. = O.C.— po pogoju, ∠ DOC = ∠AOB- navpično), to je ∠ ACD = ∠KABINA, in ker navzkrižno ležijo na ravnih črtah AB, CD in sekanto A.C., To AB vzporedno DC. Podobno dokažemo vzporednost premic B.C. in A.D. Torej, ABCD je po definiciji paralelogram. B.C. = AD, AB = CD(v paralelogramu sta nasprotni stranici enaki), A.C.- običajno za trikotnike ACD in KABINA, torej sta na treh straneh enaka. Q.E.D.

Naloga 3. Dokaži, da je mediana, narisana na osnovo enakokrakega trikotnika, simetrala kota, ki je nasproti osnovki, in je prav tako pravokotna na osnovo.

Koti, ki jih tvorita mediana in osnova, se bodo imenovali "spodnji", mediana in stranice - "zgornji".

Dokaz: stranski trikotniki na sliki so enaki na treh stranicah, iz česar sledi, da so, prvič, "zgornji" koti enaki (dokazali so, da simetrala), drugič, "spodnji" koti, skupaj kot sosednji dajejo 180 0 in torej enaka v 90 0 vsak (dokazana pravokotnost). Q.E.D.

Naloga 4. Dokaži, da sta mediani, potegnjeni na stranske stranice enakokrakega trikotnika, enaki.

Trikotniki, ki jih tvorijo mediane, osnova in spodnje polovice stranskih strani prvotnega trikotnika, se imenujejo "spodnji"

Dokaz: kota na dnu enakokrakega trikotnika sta enaka, zato sta »spodnja« trikotnika enaka po stranicah in kotu med njima, kar pomeni enakost narisanih median. Q.E.D.

Naloga 5. Dokaži, da sta simetrali, ki potekata iz oglišč osnovice enakokrakega trikotnika, enaki.

Vsi koti, označeni na sliki, so seveda enaki, čeprav so označeni z različnimi loki

Dokaz:"Spodnji" trikotnik je enakokrak, kar izhaja iz enakosti kotov na njegovem dnu, "stranski" trikotnik je enak po stranicah (enaki iz zgoraj dokazanih simetral) in dveh kotih (prvi so enaki po pogoju, drugi so navpične), zato so tudi preostali deli simetral med seboj enaki, kar pomeni, da so enake celotne simetrale. Q.E.D.

Naloga 6. Dokaži, da je dolžina odseka, ki povezuje razpolovišči obeh stranic trikotnika, enaka polovici tretje stranice.

Čiste stranice bomo imenovali "osnove", prečrtane pa "stranice".

Dokaz: stranski strani malega in velikega trikotnika na sliki sta v razmerju 1 : 2, poleg tega imata en skupni kot, kar pomeni, da sta si po drugem atributu podobni s koeficientom podobnosti 1 : 2, zato sta osnovici razmerje 1:2. Kar je bilo treba dokazati.

Naloga 7. Dokaži, da diagonala paralelograma deli na dva enaka trikotnika.

Paralelogram z diagonalo, verjetno ni več kaj dodati

Dokaz: Nasprotni stranici paralelograma sta enaki, diagonala je tem trikotnikom skupna stranica, torej so na treh stranicah enaki. Q.E.D.

Naloga 8. Dokaži, da je mediana pravokotnega trikotnika, potegnjena na hipotenuzo, enaka polovici hipotenuze.

Z drugimi besedami, mediana je narisana iz vrha pravega kota

Dokaz:če okoli danega pravokotnega trikotnika opišemo krog, potem bo pravi kot trikotnika, včrtanega v ta krog, opisal polkrog, zato bo hipotenuza premer tega kroga, polovice hipotenuze in mediana pa dani za nas bodo v problemu radiji, torej so vsi enaki. Q.E.D.

Naloga 9. Dokaži, da sta tangenti, narisani na krožnico iz ene točke, enaki.

Dodatna konstrukcija: povežite točko C s točko O (miselno)

Dokaz: koti B in A ravne črte (polmeri kroga, narisanega na točko nihanja, so pravokotni na tangente), kar pomeni pravokotne trikotnike AOC in BOC enaka v hipotenuzi (stran, ki si jo predstavljamo, jima je skupna O.C.) in kraka (polmeri kroga O.B. = O.A.), kar pomeni A.C. = C.B.. Q.E.D.

Problem 10. Dokaži, da je premer, ki poteka skozi središče tetive kroga, pravokoten nanj.

Premica, ki povezuje dve točki na sliki, je mediana trikotnika, ki ga bomo obravnavali

Dokaz: v enakokrakem trikotniku, ki ga tvorijo presečišča tetive s krogom in središče tega kroga, bo upodobljena mediana višina, kar pomeni, da je premer, ki vsebuje to višino, pravokoten na tetivo. Q.E.D.

Problem 11. Dokažite, da če imata dve krožnici skupno tetivo, potem je premica, ki poteka skozi središče teh krožnic, pravokotna na to tetivo.

Miselno povežite vse točke, označene na sliki, imenujemo točko presečišča vodoravne in navpične črte H

Dokaz: trikotniki O 1 A.O. 2 in O 1 B.O. 2 sta na treh straneh enaka, torej ∠ HO 2 A = ∠HO 2 B, nato trikotniki HAO 2 in HBO 2 sta na obeh stranicah in kotu med njima enaka, kar pomeni ∠ AHO 2 = ∠BHO 2, in skupaj dva enaka kota lahko dasta 180 0 le, če je vsak od njiju enak 90 0. Q.E.D.

Problem 12. Dokaži, da če je krog lahko včrtan štirikotniku, potem sta vsoti dolžin njegovih nasprotnih stranic enaki.

Obkrožen štirikotnik. Imenujmo ga ABCD. Naj bodo M, E, X in L tangentne točke

Dokaz: Uporabimo izrek o tangentnih odsekih (naloga 9). VC = VR, SR = CH, DX = D.L. in AT = AK. Povzemimo strani AB in CD: AB + CD= (A.M.+ M.B.) + (DX+ XC) = AL+ BITI+ D.L.+ C.E.= (AL+ LD) + (BITI+ E.C.) = AD+ B.C. Q.E.D.

Problem 13. Dokaži, da če je okrog štirikotnika mogoče opisati krog, potem sta vsoti njegovih nasprotnih kotov enaki.

Circumcircle

Dokaz: Po izreku o včrtanem kotu je vsota nasprotnih kotov tega štirikotnika enaka 180 0, saj skupaj ležijo na celotnem krogu, katerega stopinjska mera je 360 ​​0. Q.E.D.

Problem 14. Dokaži, da če je okrog trapeza mogoče opisati krog, potem je trapez enakokrak.

Dokaz: vsota nasprotnih kotov štirikotnika, včrtanega v krog, je enaka α + β = 180 0 (glej nalogo 13), je tudi vsota kotov na stranski stranici trapeza enaka α + γ = 180 0 (ti koti so enostrani z vzporednima osnovama in sekantno stranico), iz primerjave teh formul ugotovimo, da β = γ , to pomeni, da so koti na dnu takšnega trapeza enaki in je resnično enakokrak. Q.E.D.

Problem 15. Na kvadrat ABCD točke TO in E- središča stranic AB in AD oz. Dokaži to KD pravokotno C.E..

1. izrek . Velikost včrtanega kota je enaka polovici velikosti središčnega kota, ki ga sega isti lok.

Dokaz . Najprej razmislimo o včrtanem kotu ABC, stran B.C. ki je premer kroga in središčni kot AOC(slika 5).

Ker segmenti A.O. in B.O. so polmeri kroga, nato trikotnika AOB– enakokraki in kot ABO enak kotu OAB. Ker kot AOC je zunanji kot trikotnika AOB, potem so enakosti resnične

Tako je v primeru, ko ena od stranic včrtanega kota poteka skozi središče kroga, 1. izrek dokazan.

Zdaj razmislite o primeru, ko središče kroga leži znotraj včrtanega kota (slika 6).

in izrek 1 je v tem primeru dokazan.

Še vedno je treba razmisliti o primeru, ko središče kroga leži zunaj včrtanega kota (slika 7).

V tem primeru so enakosti resnične

ki zaključuje dokaz izreka 1.

Izrek 2 . Velikost kota, ki ga tvorijo tetive, ki se sekajo, je enaka polovici vsote velikosti lokov, sklenjenih med njegovimi stranicami.

Dokaz . Razmislite o sliki 8.

Zanima nas kot AED E akordi AB in CD. Ker kot AED– zunanji kot trikotnika POSTELJO, in koti CDB in ABD

Q.E.D.

Izrek 3 . Velikost kota, ki ga tvorijo sekante, ki se sekajo zunaj kroga, je enaka polovici razlike v velikostih lokov, zaprtih med stranicami tega kota.

Dokaz . Razmislite o sliki 9.

Zanima nas kot POSTELJO, ki nastane s sekanjem v točki E sekante AB in CD. Ker kot ADC– zunanji kot trikotnika ADE, in koti ADC , DCB in DAB sta včrtana kota, potem veljajo enakosti

Q.E.D.

Izrek 4 . Velikost kota, ki ga tvorita tangenta in tetiva, ki poteka skozi točko stika, je enaka polovici velikosti loka, sklenjenega med njunima stranicama.

Dokaz . Razmislite o sliki 10.

Zanima nas kot BAC ki ga tvori tangenta AB in akord A.C.. Zaradi AD je premer, ki poteka skozi stično točko, in kot ACD je včrtan kot, ki temelji na premeru, nato na kotih DAB in DCA– naravnost. Zato so enakosti resnične

Q.E.D.

Izrek 5 . Velikost kota, ki ga tvorita tangenta in sekans, je enaka polovici razlike v velikostih lokov, sklenjenih med stranicama tega kota.

Dokaz . Razmislite o sliki 11.

Zanima nas kot POSTELJO ki ga tvori tangenta AB in sekanto CD. Upoštevajte, da je kot BDC– zunanji kot trikotnika DBE, in koti BDC in BCD so včrtani koti. Še več, koti DBE in DCB, na podlagi izreka 4, sta enaka. Zato so enakosti resnične

Dva kota imenujemo sosednja, če imata eno stran skupno in sta drugi strani teh kotov komplementarni žarki. Na sliki 20 sta kota AOB in BOC sosednja.

Vsota sosednjih kotov je 180°

Izrek 1. Vsota sosednjih kotov je 180°.

Dokaz. Žarek OB (glej sliko 1) poteka med stranicama razgrnjenega kota. Zato ∠ AOB + ∠ BOS = 180°.

Iz izreka 1 sledi, da če sta dva kota enaka, sta tudi njuna sosednja kota enaka.

Navpični koti so enaki

Dva kota se imenujeta navpična, če sta strani enega kota komplementarni žarki strani drugega. Koti AOB in COD, BOD in AOC, ki nastanejo v presečišču dveh ravnih črt, so navpični (slika 2).

Izrek 2. Navpična kota sta enaka.

Dokaz. Razmislimo o navpičnih kotih AOB in COD (glej sliko 2). Kot BOD je priležen k vsakemu od kotov AOB in COD. Po izreku 1 je ∠ AOB + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.

Iz tega sklepamo, da je ∠ AOB = ∠ COD.

Posledica 1. Kot, ki meji na pravi kot, je pravi kot.

Oglejmo si dve sekajoči se premici AC in BD (slika 3). Oblikujejo štiri vogale. Če je eden od njiju ravni (kot 1 na sliki 3), potem so tudi preostali koti pravi (kota 1 in 2, 1 in 4 sta sosednja, kota 1 in 3 sta navpična). V tem primeru pravijo, da se te črte sekajo pravokotno in se imenujejo pravokotne (ali medsebojno pravokotne). Pravokotnost premic AC in BD označimo takole: AC ⊥ BD.

Simetrala pravokotna na odsek je premica, ki je pravokotna na ta odsek in poteka skozi njegovo središče.

AN - pravokotno na premico

Vzemimo premico a in točko A, ki ne leži na njej (slika 4). Povežimo točko A z odsekom s točko H s premico a. Odsek AN imenujemo navpičnica, ki je narisana iz točke A na premico a, če sta premici AN in a pravokotni. Točka H se imenuje osnova navpičnice.

Risanje kvadrata

Naslednji izrek drži.

Izrek 3. Iz katere koli točke, ki ne leži na premici, je mogoče na to premico potegniti pravokotno in poleg tega samo eno.

Za risanje pravokotnice iz točke na premico na risbi uporabimo risalni kvadrat (slika 5).

Komentiraj. Formulacija izreka je običajno sestavljena iz dveh delov. En del govori o danem. Ta del se imenuje pogoj izreka. Drugi del govori o tem, kaj je treba dokazati. Ta del se imenuje zaključek izreka. Na primer, pogoj izreka 2 je, da so koti navpični; zaključek - ti koti so enaki.

Vsak izrek je mogoče podrobno izraziti z besedami, tako da se njegov pogoj začne z besedo »če«, zaključek pa z besedo »potem«. Na primer, izrek 2 je mogoče podrobno navesti takole: "Če sta dva kota navpična, potem sta enaka."

Primer 1. Eden od sosednjih kotov je 44°. Čemu je enako drugo?

rešitev. Označimo stopinjsko mero drugega kota z x, takrat po izreku 1.
44° + x = 180°.
Če rešimo dobljeno enačbo, ugotovimo, da je x = 136°. Zato je drugi kot 136°.

Primer 2. Naj bo kot COD na sliki 21 45°. Kakšna sta kota AOB in AOC?

rešitev. Kota COD in AOB sta navpična, zato sta po izreku 1.2 enaka, tj. ∠ AOB = 45°. Kot AOC je sosednji kotu COD, kar po 1. izreku pomeni.
∠ AOC = 180° - ∠ COD = 180° - 45° = 135°.

Primer 3. Poišči sosednja kota, če je eden od njiju 3-krat večji od drugega.

rešitev. Označimo stopinjsko mero manjšega kota z x. Potem bo stopinjska mera večjega kota 3x. Ker je vsota sosednjih kotov enaka 180° (1. izrek), potem je x + 3x = 180°, od koder je x = 45°.
To pomeni, da sta sosednja kota 45° in 135°.

Primer 4. Vsota dveh navpičnih kotov je 100°. Poiščite velikost vsakega od štirih kotov.

rešitev. Naj sta slika 2 enaka navpičnim kotom COD na AOB (izrek 2), kar pomeni, da sta tudi njuni stopinjski meri. Zato je ∠ COD = ∠ AOB = 50° (njuna vsota po pogoju je 100°). Kot BOD (tudi kot AOC) je sosednji kotu COD, zato je po izreku 1
∠ BOD = ∠ AOC = 180° - 50° = 130°.